I thought I'd say a little more about the topic of undefined equity, using a variant of an old position from rec.games.backgammon.
Consider the position below. It's the first game of a seven-point
match. Note that the position is symmetrical. What's the cube action?
  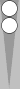 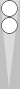 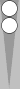 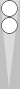  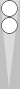  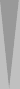 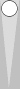 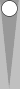 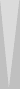 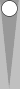      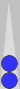 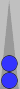 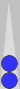 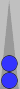 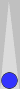 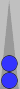   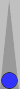 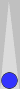  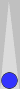    |
| ||||
| XGID=aBBBBAB-AA-A--a-aa-babbbbA:0:0:1:00:0:0:0:7:10 | |||||
| Blue on roll, cube action? | |||||
Let's start by using our normal backgammon intuition to assess the position. Since Blue has 25 dancing rolls, it doesn't seem possible that it could be a pass for White. What about the double? Every sequence that doesn't start with a dance loses Blue's market, unless Blue rolls 51 or 52 (lifting his 5pt blot) and White enters with 55. Furthermore these sequences are hugely gammonish. It's hard to weigh this against the whopping 25 dancing rolls, but it seems plausible that this could be a double, maybe even a big double.
Let's see what an XG rollout says.
| Analyzed in Rollout | No double | Double/Take |
| Player Winning Chances: | 58.19% (G:48.35% B:8.22%) | 58.02% (G:48.31% B:7.89%) |
| Opponent Winning Chances: | 41.81% (G:33.71% B:5.16%) | 41.98% (G:33.86% B:5.49%) |
| Cubeless Equities | +0.348 | +0.693 |
| Cubeful Equities | ||
| No double: | +0.328 (-0.023) | ±0.016 (+0.312..+0.343) |
| Double/Take: | +0.351 | ±0.019 (+0.332..+0.369) |
| Double/Pass: | +1.000 (+0.649) | |
| Best Cube action: Double / Take | ||
| Rollout details | ||
| 1296 Games rolled with Variance Reduction. Dice Seed: 271828 Moves: 3-ply, cube decisions: XG Roller | ||
| Double Decision confidence: | 96.9% | |
| Take Decision confidence: | 100.0% | |
| Duration: 10 minutes 27 seconds | ||
eXtreme Gammon Version: 2.19.208.pre-release, MET: Kazaross XG2
O.K., so this accords with our intuition. Maybe a small double, certainly a huge take.
But let's look ahead a little more. What happens if Blue dances? Then White is faced with exactly the same decision that Blue is faced with in the original position. If the original position is D/T, then the position after a dance must also be D/T. Seems like the cube could get up to a high value pretty quickly. Of course, since it's a seven-point match, the cube can't get higher than 8. So what happens if we change the score to 15a15a? Let's see what an XG rollout says:
    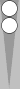 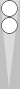 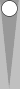 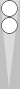     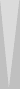 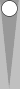 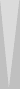         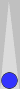 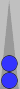 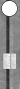 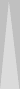 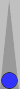 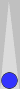 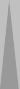 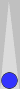    |
| ||||
| XGID=aBBBBAB-AA-A--a-aa-babbbbA:0:0:1:00:0:0:0:15:10 | |||||
| Blue on roll, cube action? | |||||
| Analyzed in Rollout | No double | Double/Take |
| Player Winning Chances: | 58.03% (G:48.30% B:7.46%) | 58.17% (G:48.20% B:7.36%) |
| Opponent Winning Chances: | 41.97% (G:33.60% B:4.94%) | 41.83% (G:33.72% B:4.77%) |
| Cubeless Equities | +0.338 | +0.688 |
| Cubeful Equities | ||
| No double: | +0.221 (-0.266) | ±0.014 (+0.208..+0.235) |
| Double/Take: | +0.488 | ±0.016 (+0.471..+0.504) |
| Double/Pass: | +1.000 (+0.512) | |
| Best Cube action: Double / Take | ||
| Rollout details | ||
| 2592 Games rolled with Variance Reduction. Dice Seed: 271828 Moves: 3-ply, cube decisions: XG Roller | ||
| Double Decision confidence: | 100.0% | |
| Take Decision confidence: | 100.0% | |
| Duration: 19 minutes 17 seconds | ||
eXtreme Gammon Version: 2.19.208.pre-release, MET: Kazaross XG2
Whoa! That made a big difference. Now the rollout says it's a huge double. Those big cubes are evidently having a significant effect.
O.K., now comes the obvious question. What happens if we try a money-game rollout?
   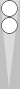 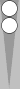 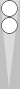 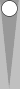     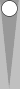 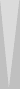 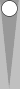 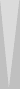             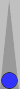 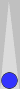      |
| ||||
| XGID=aBBBBAB-AA-A--a-aa-babbbbA:1:1:1:00:0:0:0:0:10 | |||||
| Blue on roll, cube action? | |||||
| Analyzed in Rollout | No redouble | Redouble/Take |
| Player Winning Chances: | 58.06% (G:48.55% B:7.71%) | 58.13% (G:48.56% B:7.52%) |
| Opponent Winning Chances: | 41.94% (G:33.77% B:5.24%) | 41.87% (G:33.79% B:5.25%) |
| Cubeless Equities | +0.334 | +0.666 |
| Cubeful Equities | ||
| No redouble: | +0.958 (-0.042) | ±0.041 (+0.917..+0.998) |
| Redouble/Take: | +1.582 (+0.582) | ±0.058 (+1.525..+1.640) |
| Redouble/Pass: | +1.000 | |
| Best Cube action: Redouble / Pass | ||
| Rollout details | ||
| 46656 Games rolled with Variance Reduction. Dice Seed: 271828 Moves: 3-ply, cube decisions: XG Roller | ||
| Double Decision confidence: | 98.0% | |
| Take Decision confidence: | 100.0% | |
| Duration: 2 hours 22 minutes | ||
eXtreme Gammon Version: 2.19.208.pre-release
You've got to be kidding me!! A huge pass? No way! Could this possibly be correct?
The answer is no. This is a rare case where we can actually analyze a complex contact position "by hand" as it were. Let us hypothesize, for the sake of argument, that the "perfect play" cube action in this position, is D/P, and let's draw out the logical consequences. A pass of course gives White an equity of –1. On the other hand, suppose that White takes. Then, 25/36 of the time, Blue dances, and then by hypothesis, the correct cube action is D/P so White's equity is +2. So the contribution to White's equity from these sequences is 50/36. Now suppose that Blue hits. Then we can't analyze exactly what happens, but we can say this: White has the option of adopting the strategy of refusing to redouble again under any circumstances. This may not be White's best strategy, but it is one strategy that is available to her. If she adopts this strategy, then at worst she loses 6 points (if she gets backgammoned). Therefore, White's equity from these sequences is at worst 11/36 × (–6) = –66/36. If we add this to 50/36 then we get a grand total of –16/36. This is not White's equity, but it's a lower bound on White's equity. Whatever White's true equity is, it can't be any worse than this. And since –16/36 > –1, it follows that White does better by taking than by passing. So it can't be a pass. This contradicts our initial hypothesis that the perfect cube action is D/P. Therefore, our initial hypothesis must have been incorrect, and the perfect play cube action cannot be D/P.
On the other hand, if the perfect play cube action is D/T, then an argument along the lines of the one presented by Gary Wong in that old rec.games.backgammon article applies to show that the equity is unbounded.
What does this say about the concept of "perfect play"? If there is such a thing as perfect play, then White's perfect play after a double by Blue must be either "take" or "pass" since those are her only two options. But we've just shown that "pass" can't be the right answer, and "take" leads to undefined equities. Therefore "perfect play" doesn't make sense in this position.
As a final comment, note that even though the above money-game rollout involves 46656 trials, the confidence interval is still huge! This is on account of the large cubes. Below, I've reproduced XG's "Rollout Statistics" to show how often the cube gets up to some gigantic value. Note that XG has a built-in cap of 1024 on the cube value, or else the numbers would have been even more crazy.
XGID=aBBBBAB-AA-A--a-aa-babbbbA:1:1:1:00:0:0:0:0:10
Redouble/Take Non VR Equity: +1.957 (Cost: +3.913)
Cube Win BG Win G Win S Cash Pass Lose S Lose G Lose BG D/T D/P Take % D/T D/P Take %
2
4 1,785 9,923 1,658 461 7 13 1 32,808 461 98.61%
8 1 16 19 396 1,407 6,884 1,258 22,827 396 98.29%
16 883 4,768 1,047 249 9 14 15,857 249 98.45%
32 10 8 204 699 3,357 561 11,018 204 98.18%
64 430 2,318 533 125 9 7,603 125 98.38%
128 6 8 107 330 1,575 287 5,290 107 98.02%
256 419 2,098 460 406 6 1,443 263 195 406 32.45%
512+ 1 37 29 104 23 1 49 29 62.82%