White is Player 2 score: 0 pip: 30 Unlimited Game Jacoby Beaver pip: 50 score: 0 Blue is Player 1
XGID=----CDC---------------eee-:0:0:1:00:0:0:3:0:10
Blue on roll, cube action?

We have already handled to a good extent pips v. pips racing situations via the Keith Count. We have also seen the behind the scenes math to roll versus roll races. The next thing we need to touch on to help complete our racing understanding arsenal is what to do in pips v. rolls situations.

First, a couple common sense exercises to make a point.

		White is Player 2 score: 0 pip: 15 Unlimited Game Jacoby Beaver pip: 15 score: 0 Blue is Player 1
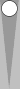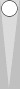XGID=-O-----------------aaa----:1:1:1:00:0:0:3:0:10
Blue on roll, cube action?

Who would you rather be in this situation, the top or the bottom player. Why? They both have the same pip count and the bottom player owns the cube and is on roll!? How often do you expect the bottom player to win?

		White is Player 2 score: 0 pip: 45 Unlimited Game Jacoby Beaver pip: 50 score: 0 Blue is Player 1
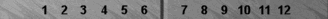XGID=-BCBC-D------------bbcbba-:1:1:1:55:0:0:3:0:10
Blue to play 55

Consider the following position:

		White is Player 2 score: 0 pip: 0 Unlimited Game Jacoby Beaver pip: 15 score: 0 Blue is Player 1
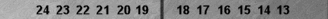XGID=-O------------------------:0:0:1:00:0:0:3:0:10
Blue on roll, cube action?

How many rolls on average will it take to bear off all 15 checkers off of the ace point? If you never rolled doubles it would be 8 and thanks to computers we can feed this through and find out that the actual number of rolls is about 7. Now, if we take the average number of rolls it takes to get those 15 checkers off, 7 rolls, and multiple it by the average number of pips per roll 8.167, the product is almost exactly 57. This gives us our first rule regarding the effective pip count or epc.

This is how the effective pip count is defined: The average number of rolls required to bear off all your checkers multiplied by the average pip value of a roll (49/6 pips). A player's EPC is equal to his actual pip count plus the wastage of the position.

Here is a chart rounded to the nearest full percent of your cubeless winning chances in any pure roll v. roll situation.

The optimal position you try to reach when bearing in during a straight race is the 7-5-3 position. This position gives the least amount of wastage for the 15 checker model. (Ask if he knows the ideal position and why)

		White is Player 2 score: 0 pip: 79 Unlimited Game Jacoby Beaver pip: 79 score: 0 Blue is Player 1
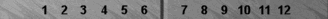XGID=----CEG------------gec----:0:0:1:00:0:0:3:0:10
Blue on roll, cube action?

This is what Walter Trice referred to as a Nice Position. A nice position is one where you have all of your checkers well distributed over the 6, 5, and 4 points. This also leads us to our second rule concerning effective pip counts:

To get our effective pipcount then in the position above we would start with the regular pip count of 79 and then add 7 effective pips to that count to get our epc of 86. Here are a few more examples of 'nice' positions noting that you still waste about 7 pips even when you have a lot fewer checker left, more on that later.

		White is Player 1 score: 0 pip: 55 Unlimited Game Jacoby Beaver pip: 60 score: 0 Blue is Player 2
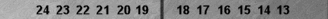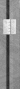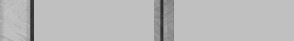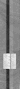XGID=----ACF------------cfc----:0:0:-1:00:0:0:3:0:10
Blue on roll, cube action?

		White is Player 1 score: 0 pip: 39 Unlimited Game Jacoby Beaver pip: 52 score: 0 Blue is Player 2
XGID=----CCB------------ddb----:0:0:-1:00:0:0:3:0:10
Blue on roll, cube action?

The least amount of pips any position can waste is just over 4 pips. For example the position below wastes above 4.5 pips for the bottom player and 4.3 for the top player. This is important because it gives you a good way of estimating other positions. Now you know that no position wastes less than 4 pips and that the nice positions waste 7 pips so once you start working with the inbetween positions you'll get a much better feel for them.

The third rule we need before we go any further with the epc is:

		White is Player 1 score: 0 pip: 42 Unlimited Game Jacoby Beaver pip: 44 score: 0 Blue is Player 2
XGID=-BBBBBB------------cbabbb-:0:0:-1:00:0:0:3:0:10
Blue on roll, cube action?

The bottom position is your clasical flat position and the top position is a near flat position. Since the 4pt has only one checker and you risk voiding it and wasting subsequent fours you should be able to reason that the wastage of the top player is slightly above 10 pips.

Now to the money question, how do we convert the epc to proper cube action?

• The point of last take for the trailer is when he is down a number of effective pips equal to the number of rolls to go minus three.

• You can send an initial double when you are within' 2 effective pips of his point of last take and a recube when you are within' 1 effective pip of his point of last take.